Online height transformation in the border areas of Germany, Austria and Switzerland (D-A-CH height transformation) — Standard mode

Explanations

Background on height systems

Heights and zero-level surfaces in Germany, Austria and Switzerland differ for historical and geophysical reasons.

What we experience as “heights” in daily life (physical heights, “heights above sea level”) depends on the Earth’s gravity field. The concept of the geoid, i.e., the hypothetical surface of an undisturbed ocean extended at land, is understood as the idealized reference surface for heights.

Consequently, models of (quasi)geoid heights are used as height reference surface for GNSS-based height determination, i.e., for the transformation of observed ellipsoidal heights into physical heights (see Fig. 1). In the generalized formula

h = H + U

h is the ellipsoidal height, H denotes the respective physical height, and U represents the undulation value of the corresponding height reference surface (i.e., geoid height N or quasigeoid height ζ).
 

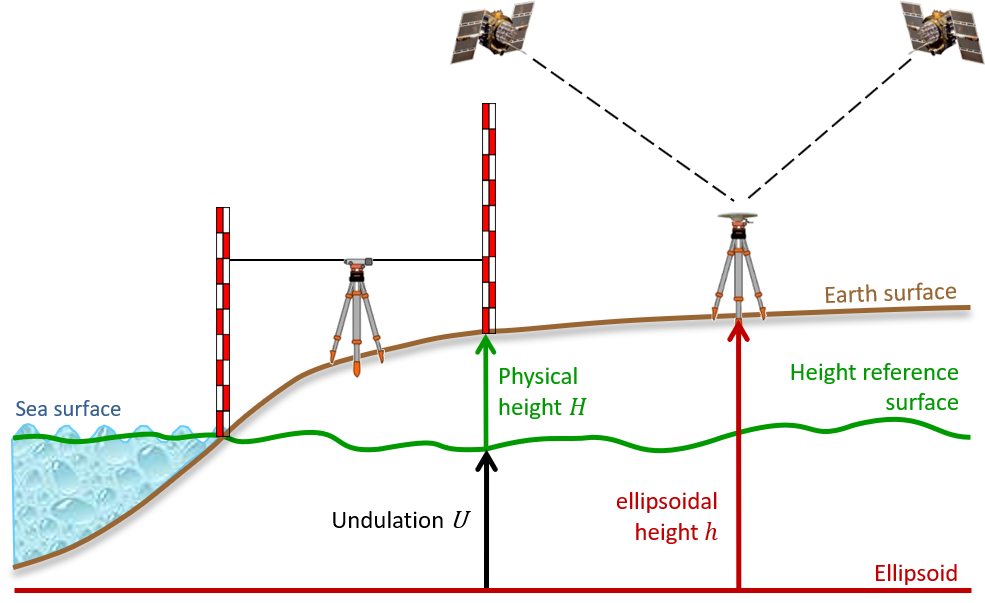
Fig. 1 Schematic view of heights and height reference surfaces

Fig. 1 Schematic view of heights and height reference surfaces
 

Unfortunately, “the” mean sea level (and, thus, “the” geoid) does not exist. The real oceans underly ocean dynamics which are driven by the hydro-mechanic settings of the coast as well as oceanographic and atmospheric parameters. Therefore, even the long-term mean sea level is not an equilibrium surface. Thus, the observed mean sea level at a specific cite does not coincide with the global mean sea level resp. geoid. The zero level of a regional or national height network and the according geoid model is always subject to a datum definition and depends on the location and epoch of the mareograph site which is taken as a reference.

Like all classical (optical) geodetic measurement techniques, height measurements need to be corrected for the influence of the local gravity field. There are various methods to do this, which lead to different results. Experts speak of different height types. Nowadays, either normal heights (e.g., Germany, system DHHN2016) and orthometric heights (e.g., Switzerland, new system LHN95) are widely used. The choice of the height type for the leveling networks of the individual countries is subject to theoretical, practical and, in some cases, historical reasons, which will not be discussed here.

Although orthometric heights and normal heights are routinely computed and provided for scientific applications in Austria and Switzerland, the official heights systems of these countries based on normal-orthometric heights (Austria, System MGI) or even uncorrected heights (Switzerland, “old” System LN02) remain to be in use.

Different height types are the prevailing reason why height differences between countries vary along the course of national borders. For example, height numbers in the Swiss system LN02 are approx. 32 cm larger than in the German system DHHN2016 close to Basel, whereas near Schaffhausen the difference is approx. 36 cm.
 

A note on “Normalnull (NN)” and “Normalhöhennull (NHN)” in Germany

For historical reasons, a number of different height systems (and height system realizations) had been used in Germany, too. Here, in the D-A-CH height transformation application, these German legacy systems are deliberately left out. A comprehensive overview can be found in Sacher and Liebsch (2018, Tab. 2.2, p. 23).

The term Normalnull (NN), which was used for the old German height systems before 1992 (except the GDR), does not refer to the application of normal heights (in fact, these heights were normal-orthometric!) but to the definition of the zero level, the Normal Amsterdam’s Peil (NAP).

In contrast, the zero level surface of the normal heights since 1992 (DHHN92, DHHN2016) is refered to as Normalhöhennull (NHN). It is realized by quasigeoid models (DHHN92: GCG05/GCG2011, DHHN2016: GCG2016).
 

Further information / Literature

DE – Germany

AT - Austria

CH – Switzerland

 

back

Imprint

Privacy

to top