Online-Höhentransformation für den Übergang zwischen den nationalen Systemen von Deutschland, Österreich und der Schweiz im Grenzgebiet (D-A-CH-Höhentransformation) — Expertenmodus

Erläuterungen

Hintergrund zu Höhensystemen

Höhen und Höhenbezugsflächen in Deutschland, Österreich und der Schweiz unterscheiden sich aus historischen und geophysikalischen Gründen.

Was wir im Alltag als „Höhen” (physikalische Höhen, „Höhen über Meeresspiegel”) erfahren, wird durch das Schwerefeld beeinflusst. Die idealisierte Bezugsfläche für Höhen ergibt sich aus dem Konzept des Geoids, d.h. der hypothetischen Oberfläche eines unter den Landmassen erweiterten ungestörten Ozeans.

Modelle von Geoid- bzw. Quasigeoidhöhen werden daher heute als Bezugsfläche für GNSS-gestützte Höhenbestimmung, d.h. zur Transformation der beobachteten ellipsoidischen Höhen in physikalische Höhen, verwendet (Abb. 1). In der verallgemeinerten Formel

h = H + U

bezeichnet h die ellipsoidische Höhe, H die jeweilige physikalische Höhe und U den Undulationswert der dazugehörigen Höhenbezugsfläche (d.h. Geoidhöhe N bzw. Quasigeoidhöhe ζ).
 

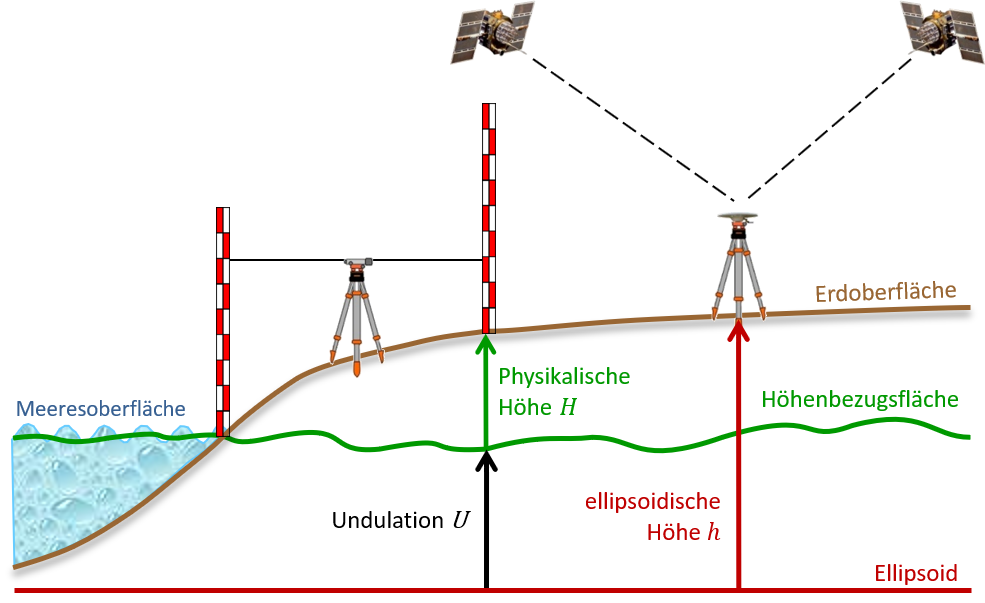
Abb. 1 Schematische Darstellung von Höhen und Höhenbezugsflächen

Abb. 1 Schematische Darstellung von Höhen und Höhenbezugsflächen
 

Leider gibt es nicht „den” einen mittleren Meeresspiegel (und damit „das” eine Geoid). Die realen Meere unterliegen einer Ozeandynamik, die durch hydromechanische Eigenschaften der Küste sowie ozeanographische und atmosphärische Parameter angetrieben wird. Daher ist selbst der langfristige mittlere Meeresspiegel keine Gleichgewichtsfläche. Der beobachtete mittlere Meeresspiegel an einem spezifischen Ort weicht vom globalen mittleren Meeresspiegel bzw. Geoid ab. Das Nullniveau eines regionalen bzw. nationalen Höhennetzes und des damit verknüpften Geoidmodells unterliegt immer einer Datumsdefinition und hängt von Ort und Zeitraum des mittleren Meeresspiegels an der Pegelstation ab, die als Referenz verwendet wird.

Höhenmessungen müssen, wie alle klassischen (optischen) geodätischen Messverfahren, um den Einfluss des lokalen Schwerefeldes korrigiert werden. Die Ausgleichung von nationalen und kontinentalen Höhennetzen geschieht dann in Form von sogenannten geopotentiellen Koten C bzw. Potentialdifferenzen ΔW = g ⋅ ΔH zwischen zwei Punkten (d.h. in Einheiten der potentiellen Energie in Bezug auf eine Einheitsmasse, also „Beschleunigung mal Weg” statt „Kraft mal Weg”). Zur Umrechnung in eine metrische Höhe muss dann wieder durch einen Schwerewert geteilt (normiert) werden. Je nachdem, welcher Schwerewert zur Korrektion und zur Normierung verwendet wird, spricht man von unterschiedlichen Höhenarten. Heutzutage gebräuchlich sind entweder Normalhöhen (z.B. Deutschland, System DHHN2016) und orthometrische Höhen (z.B. Schweiz, neues System LHN95). Die Wahl der Höhenart für die Höhennetze in den jeweiligen Ländern hat theoretische, praktische und z.T. auch historische Gründe, worauf an dieser Stelle nicht eingegangen werden soll. Einen umfassenden Überblick über die Höhenarten geben Schlatter und Marti (2007, insbesondere Abschnitte 2.3, 2.6 und Abb. 2.6-1), während Tab. 1 eine Zusammenfassung enthält.
 

Tab. 1 Wesentliche Eigenschaften und Definitionen von Höhenarten und Höhenbezugsflächen. Eine Darstellung der in den Formelzeichen verwendeten Punkthöhen kann Abb. 2 entnommen werden.

Attribut Unkorrigierte Höhen Normalorthometrische Höhen HNO Normalhöhen HN Orthometrische Höhen HO
Höhenbezugsfläche Implizit Implizit Quasigeoid Geoid
Undulation Implizit Implizit Höhenanomalie (Quasigeoidhöhe) ζ Geoidhöhe N
Schwerekorrektionen an den beobachteten nivellitischen Höhen Keine Nur sphäroidisch (Normalschwere) Freiluftanomalien (tatsächlicher Schwerewert) Freiluftanomalien (tatsächlicher Schwerewert)
Theoretischer Schleifenschlussfehler? Ja Ja Nein Nein
Basiert auf echten geopotentiellen Koten C? Nein Nein Ja Ja
Schwerewert GH zur Skalierung der geopotentiellen Kote auf metrischen Höhenwert
H = C/GH		 Nicht zutreffend Nicht zutreffend Mittlere Normalschwere entlang der Lotlinie zwischen Ellipsoid und Telluroid γ(Q0,Q) Mittlere tatsächliche Schwere (approximiert) entlang der Lotlinie zwischen Geoid und Erdoberfläche g(P0,P)
Definition des Störpotentials T (tatsächliches minus normales Potential) für die Höhenbezugsfläche Nicht zutreffend Nicht zutreffend Auf der Erdoberfläche TP Auf dem Geoid T(P0)
Schwerewert GU zur Skalierung des Störpotentials auf metrischen Undulationswert
U = T/GU		 Nicht zutreffend Nicht zutreffend Normalschwere auf dem Telluroid γQ (bzw. auf der Erdoberfläche γP ohne Genauigkeitsverlust) Normalschwere auf dem Ellipsoid γ0
Hypothesenfrei? Ja Ja Ja Nein

 

Abb. 2 Visualisierung der Punkthöhen in den Formeln für Höhen und Undulationen gemäß Tab. 1

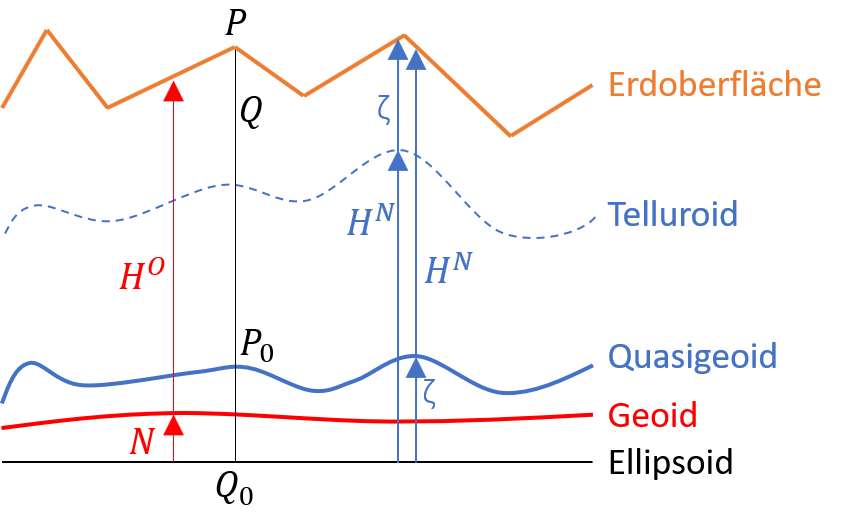
Abb. 2 Visualisierung der Punkthöhen in den Formeln für Höhen und Undulationen gemäß Tab. 1
 

In Österreich und der Schweiz werden orthometrische Höhen und Normalhöhen routinemäßig berechnet und für wissenschaftliche Zwecke bereitgestellt. Jedoch bleiben die auf normal-orthometrischen (Österreich, System MGI) oder sogar unkorrigierten Höhen (Schweiz, „altes” System LN02) basierenden Landeshöhensysteme weiterhin offiziell gültig.

Die unterschiedlichen Höhenarten sind der Grund, warum Höhendifferenzen verschiedener Länder entlang des Grenzverlaufs im Allgemeinen variieren. So sind z.B. Schweizer Höhenangaben im System LN02 bei Basel ca. 32 cm und bei Schaffhausen ca. 36 cm höher als im deutschen System DHHN2016.
 

Der D-A-CH-Höhentransformationsdienst

Die Anwendung erlaubt die Transformation zwischen den unterstützten Landeshöhensystemen (physikalische Höhen) und den nationalen ETRS89-Realisierungen (ellipsoidische Höhen). Die Transformationspfade sind in einem zweistufigen Ansatz entsprechend dem Schema in Abb. 3 definiert. Dabei wird die jeweilige zu transformierende Höhe zunächst, soweit notwendig, unter Verwendung der offiziellen nationalen (Quasi-)Geoidmodelle bzw. Höhentransformationsgitter in eine EVRS-kompatible Normalhöhe umgerechnet. Anschließend erfolgt eine inverse Transformation ins Zielsystem. Sofern möglich wird anhand eines alternativen Transformationspfades (z.B. über ellipsoidische Höhen) ein DELTA-Wert als Genauigkeitsindikator (analog zu einem „Schleifenschlussfehler” der Modelle im Transformationsschema) abgeleitet und ausgegeben.

Zwischen den nationalen Realisierungen der Normalhöhen sowie der aktuellen Realisierung des EVRS (EVRF2019) wurden durch die Rechenstelle zum UELN (M. Sacher, c/o BKG) ebenfalls Transformationsgitter abgeleitet. Diese weisen entlang der nationalen Grenzen typischerweise nur noch eine Variation von wenigen Millimetern auf. Für die nationalen Höhenbezugsflächen und Höhentransformationsgitter wird im Gegensatz dazu typischerweise Genauigkeiten von 1-3 cm angegeben, welche im Rahmen von Stichproben entlang der Grenze überprüft und bestätigt wurden. Konsequenterweise werden/wurden daher im „DACH-Transformationsdienst”

Da die nationalen Höhengitter nur für die jeweiligen Landesgebiete inklusiver einer kleinen Pufferzone gültig sind, wurden die grenzüberschreitenden Transformationsoperationen (wie z.B. DHHN2016 nach MGI) auf eine Zone von 4 km beiderseits der Grenze beschränkt. Umrechnungen von physikalischen in ellipsoidische Höhen innerhalb eines Landes (z.B. DHHN2016 nach ETRS89/DREF91 Realisierung 2016) sind ohne Einschränkungen möglich.
 

Geodätische Referenzrahmen in den D-A-CH-Ländern

Tab. 2 Übersicht und relevante Spezifikationen der Referenzrahmen in den D-A-CH-Ländern. Werte aus Transformationsgittern müssen addiert werden, um Höhen im Referenzrahmen der nachfolgenden Zeile zu erhalten (soweit nicht anders angegeben). Aus Gründen der Übersichtlichkeit sind die inoffiziellen Versionen in Form von Normalhöhen für Österreich und die Schweiz (vgl. Abb. 3) hier nicht aufgeführt.

Referenzrahmen Höhenart Datumspunkte Bezugspegel/
Nullniveau		 Referenzepoche Transformationsgitter Anmerkungen
Deutschland
DHHN2016
(„m ü.NHN”)		 Normalhöhe 72 Punkte NAP (1684) 2004-2013
(insb. 2006-2012)		 GCG2016 Quasigeoid
ETRS89/DREF91 Realisierung 2016 ellipsoidisch 2008.46 Höhen konsistent mit ETRF2000
Österreich
MGI
(„m ü.Adria”)		 normal-orthometrisch Hutbigl Triest (1875) 1950-2011 Höhen-Grid
AT_NAP_OH orthometrisch Hutbigl NAP (1684) 1950-2011 Austrian Geoid 2008
ETRS89/ETRF2000 Austria 2002.45 ellipsoidisch 2002.45
Schweiz
LN02
(„m ü.Meer”)		 unkorrigiert Répère Pierre du Niton (RPN) Marseille Einrechnung unter Zwang in das Netz 1861-1891 CHLN02
(nach CHTRF20xx)
LHN95 orthometrisch Zimmerwald Marseille 1993.0 CHGeo2004 Geoid LN02-Höhe von RPN fixiert
CHTRF20xx ellipsoidisch 1993.0 Höhenoffset ggü. ETRF2000

 

Abb. 3 Vereinfachtes Transformationsschema des D-A-CH-Höhentransformationsdienstes (d.h. unter Annahme einer konstanten Niveaudifferenz zwischen den nationalen Normalhöhen und EVRS bzw. zwischen den nationalen ellipsoidischen Höhen und ETRF2000)

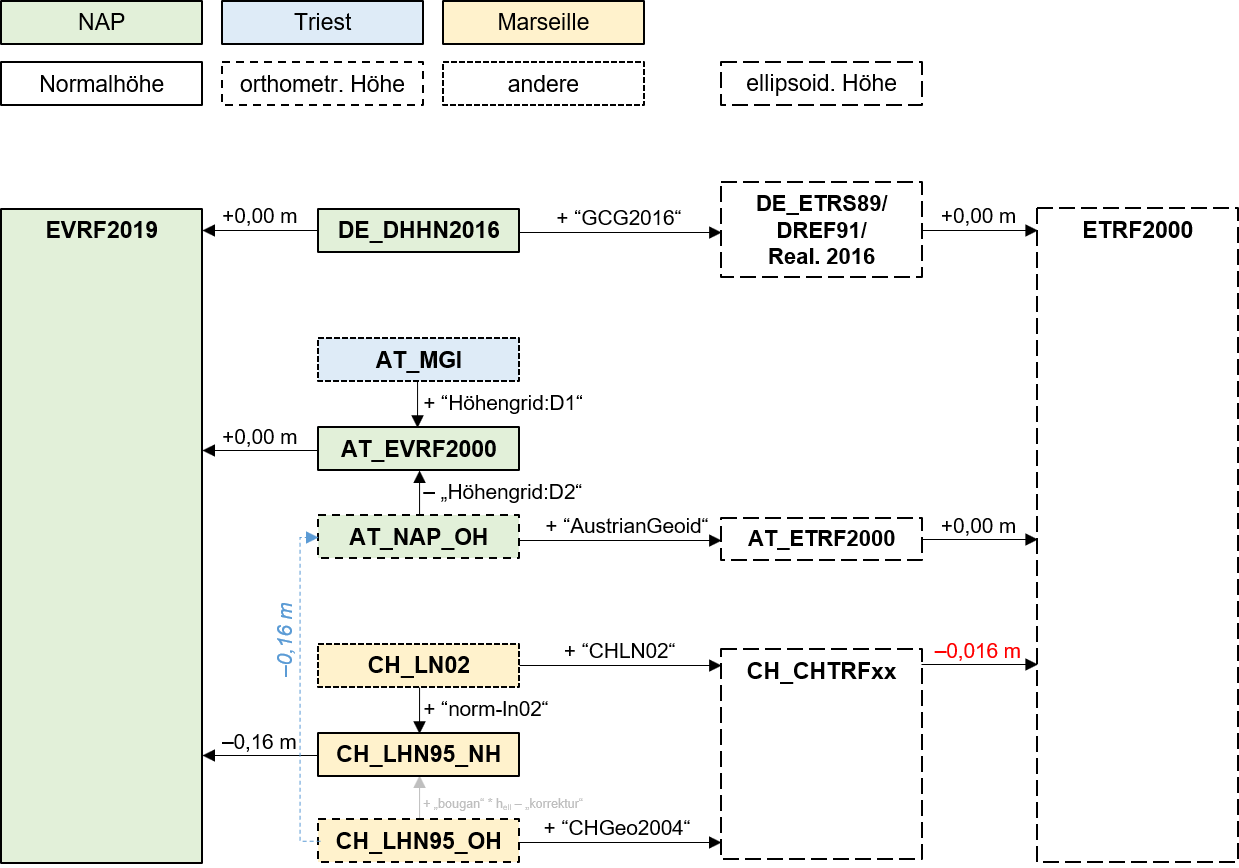
Abb. 3 Vereinfachtes Transformationsschema des D-A-CH-Höhentransformationsdienstes (d.h. unter Annahme einer konstanten Niveaudifferenz zwischen den nationalen Normalhöhen und EVRS bzw. zwischen den nationalen ellipsoidischen Höhen und ETRF2000)
 

Anmerkungen zu ”Normalnull” (NN) und ”Normalhöhennull” (NHN) in Deutschland

Aus historischen Gründen kamen auch in Deutschland verschiedene Höhenarten (und Realisierungen von Höhensystemen) zum Einsatz. Hier im D-A-CH-Höhentransformationsdienst wurden diese veralteten Systeme bewusst weggelassen. Eine umfassende Übersicht geben Sacher und Liebsch (2018, Tab. 2.2, S. 23).

Der Begriff Normalnull (NN), der für die alten deutschen Höhensysteme vor 1992 (mit Ausnahme der DDR) verwendet wurde, bezieht sich nicht auf die Anwendung von Normalhöhen (tatsächlich handelte es sich um normal-orthometrische Höhen!) sondern auf die Definition des Nullniveaus, dem Normal Amsterdams Peil (NAP).

Im Gegensatz dazu wird die Nullniveaufläche der Normalhöhen seit 1992 (DHHN92, DHHN2016) als Normalhöhennull (NHN) bezeichnet. Sie wird durch Quasigeoidmodelle (DHHN92: GCG05/GCG2011, DHHN2016: GCG2016) realisiert.
 

Weiterführende Informationen / Literatur

DE – Deutschland

AT - Österreich

CH – Schweiz

 

zurück

Impressum

Datenschutz

nach oben